
Unit Plan: Integers
Math / Grade 7
Big Ideas
Computational fluency and flexibility with numbers extend to operations with integers and decimals.
Concepts:
- Quantity
- Change
- Balance
Essential Questions
Students will keep considering…
- What is balance?
- How do you achieve balance?
- How does change affect balance?
- How does change affect quantity?
Evaluative Criteria
N/A
Monitoring Progress
Teacher will monitor progress:
Teachers can monitor progress through ongoing formative assessment including but not limited to:
- Check ins
- Teacher observation
- Homework
- Quizzes
Resources
N/A
Reflection
How will teachers and their students reflect on and evaluate the completed project?
Teacher Reflection
- What aspects of the unit went well?
- What did students struggle with?
- What did you struggle with?
- What would you add/revise the next time you taught this unit?
- Were there any unintended outcomes?
- Were students engaged?
Downloads
Stage 3 – Learning Plan
EXECUTE THE LEARNING PLAN
LEARNING EVENTS:
- These learning events/activities are suggested activities only.
- In some cases the plans are not fully completed lesson plans.
- The teacher may choose some lessons/activities to span over several lessons.
- Teachers may add, revise and adapt these lessons based on the needs of their students, their personal preferences for resources, and the use of a variety of instructional techniques.
Learning events are enriched for students when teachers consider the “WHERE TO” acronym and guiding organizer by Wiggins and McTighe.
The Learning Events should always be prefaced by focusing on the essential questions.
Acquisition-Meaning-Transfer
Day One - What Is an Integer?
The Learning Events should always be prefaced by focusing on the essential questions:
- What is balance?
- How do you achieve balance?
- How does change affect balance?
- How does change affect quantity?
What Is an Integer? (Day One)
1) To establish where students are at with their understanding of integers, asks students to brainstorm what they already know about integers – what they are, where they may have seen them, real-life applications, operations you can perform with them.
2) Guide students to understand:
- integers are positive and negative numbers
- on a number line, the negative integers are to the left of the zero and the positive integers are to the left of zero
- integers come in ‘opposite pairs;’ for example, the opposite of +3 is -3. This is because they are both equal distance from the zero on the number line
- integers have many real-life applications – golf, temperature, altitude (above and below sea level), finance, etc.
- you can work with them – add, subtract, multiply and divide them
3) Using red and yellow integer tiles, have students model integers. The red ones represent negative numbers, while the yellow represent positive.
4) Start by having the students work in partners to model a positive integer (i.e. +3) with the positive tiles only.
5) Repeat by asking students to model a negative integer, (i.e. -4), using only negative tiles.
6) Next, ask students to model a positive integer again, but tell them they have to use negative tiles as well. Answers will vary. Expect students to struggle at first with this.
7) Guide students to understand the concept of a zero pair (one red tile, and one yellow tile represent +1 and -1. This makes a zero pair because if you add the two together, they make zero).
8) Ask them to make integers using zero pairs. Reinforce that the number of zero pairs you use doesn’t matter. How many you have left over after you cancel out the zero pairs does – this is what makes the actual number. For example:
9) Have students practice making many integers using zero pairs
10) Paper pencil practice of making integers. For example:
- Give students a target integer and ask them to find as many different ways as they can to make it, using zero pairs
- Textbook practice (Math Makes Sense 7, or Math Focus 7, or Math Links 7 has some)
Day Two - Adding Integers with Integer Tiles
The Learning Events should always be prefaced by focusing on the essential questions:
- What is balance?
- How do you achieve balance?
- How does change affect balance?
- How does change affect quantity?
Adding Integers with Integer Tiles? (Day Two)
1) Review how to make integers using zero pairs. Tell students that when they do this, they are actually adding integers. Have students model +4 with zero pairs. Model what the addition sentence would be for the various ways they made it.
2) Repeat this activity with other integers. Possible ideas:
- Provide one ‘target’ number and make as many addition sentences as you can
- Have students create their addition sentences with tiles, and have others identify the corresponding addition sentence
- Provide images of integer tiles and have students identify corresponding addition sentence
3) Textbook practice – (Math Makes Sense 7, or Math Focus 7, or Math Links 7 has some)
Day Three - Adding Integers with a Number Line
The Learning Events should always be prefaced by focusing on the essential questions:
- What is balance?
- How do you achieve balance?
- How does change affect balance?
- How does change affect quantity?
Adding Integers with a Number Line (Day Three)
1) The purpose of this lesson is to show students another way to add integers. Show students a ‘regular’ addition sentence and a number line (i.e. 3+4 = 7). Ask them to explain how they would typically use this number line to show how to solve it. Look for:
- The first number (3) shows where to start on the number line
- Adding means make the number bigger, so go right on the number line
- The second number (4) shows how far to ‘jump’ from the starting number
- Where the line/arrow ends, is the sum (7)
2) Next, provide students with an integer addition sentence (i.e. (-2) + (+5) = (+3) ) and a large number line on the board. Ask them to think about what they already know about addition and think about how we might show this one on a number line. It is important that students know the sum, in order to do this at first. In other words, they need to know where they are going, in order to get there. Allow students to struggle with this for a little bit and then show them the process:
- Start at zero
- Draw an arrow from zero to the first number (-2)
- Look at the sign on the second number – NOT the operation. If it is positive, we are making the number bigger, and if it negative, we are making the number smaller. Bigger means move right on the number line, and smaller means move left.
- In this case, with (+5), draw an arrow from (-2) that moves four spaces to the left.
- The arrow should now point to the sum (+3).
3) Repeat this activity with other addition sentences. Provide students with number lines they can work on
4) Other activities (these can be done on paper, or vertically on whiteboards and windows):
- Give students various addition sentences and have them model them on number lines; do this in partners
- Have students model addition sentences on number lines and get other students to identify the addition sentences that go with them.
- Textbook practice (Math Makes Sense 7 has some)
Day Four - Adding Integers Review Using Magic Squares
The Learning Events should always be prefaced by focusing on the essential questions:
- What is balance?
- How do you achieve balance?
- How does change affect balance?
- How does change affect quantity?
Adding Integers Review Using Magic Squares (Day Four)
1) Put students in random groups of two or three and have them work vertically on whiteboards or windows to work with the magic squares
2) Explain to students what a magic square is – a grid, where each row, column and diagonal has the same sum.
3) Give students the following magic square and have them work to solve it. Ensure students show their thinking around the magic square.
4) Once students complete the first one, give them the next one.

5) To extend, ask students to make their own 3 x 3 magic square, then continue to extend to larger magic squares (4 x 4, 5 x 5, etc…)
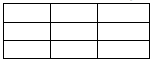
6) Follow up activity: Diamond sheet on adding integers (see below – imagine there is a box in the middle of the page where and integer addition sentence is written). The goal of this activity is to get students communicate their understanding in various ways, using the curricular competencies.
| Represent Visually | Explain in Words: |
| Describe a Real-Life Scenario | A Question You Still Have |
Day Four - Subtracting Integers with Tiles
The Learning Events should always be prefaced by focusing on the essential questions:
- What is balance?
- How do you achieve balance?
- How does change affect balance?
- How does change affect quantity?
Subtracting Integers with Tiles (Day Four)
1) Using the red and yellow tiles again, ask students to model (+4) with positive tiles. Ask students to take away (+1). What is the difference? Repeat with (-4) – (-1).
2) Have students model (+4) again with positive tiles. Ask them to take away (-1) now. Let students struggle with how to do this for a bit. Watch for what students do. They may realize they do not have any negative tiles to take away. They may add a negative tile. Walk around room and remind students what they have modelled with their tiles, if they do this. For example, if they started with four positive tiles, and add a negative, they only have (+3) now, as they created a zero pair with one of the existing tiles.
3) After a bit, redirect students to watch you. Model (+4) on the board. Ask students if they actually have any negatives to take away. Point out that they do not, so where are they going to come from? Remind students that you can add zero pairs to integers, without changing the integer. This keeps things balanced. In a subtraction sentence, the first number tells you what you start with (in this case, +4), and the second number tells you how many to take away. Sometimes you have enough (as was the case in the very first examples), and sometimes you do not (as is the case in this example). When you do not have enough, the second number tells you how many zero pairs you need to add in, in order to get what you need to take away.
- For example, in this question, (+4) – (-1), you start with four positive tiles. You do not have any negatives to take away, so you need to add one zero pair (because the second number is (-1). Now, you can take away one negative, and you are left with five positives, so the difference is (-5).
- Repeat this with various examples like this question (i.e. (+5) – (-6) or (-2) – (+4)
4) Next, ask students to model a question like this: (+4) – (+6)
- After practicing with the above examples, students will be tempted to add six zero pairs, since the second number is 6. Allow them to do this, but ask them what they have left when they take the six positives away. They should notice that something isn’t working now.
- With the whole group, model (+4). Remind them that the second number is telling them how many to take away. In this case, it is six positives. Guide them to realize they already have four positives, so they don’t need to add six zero pairs, they only need to add two of them in order to have enough positives to take away.
5) Guide students to realize that when you are subtracting integers, you need to think about the following:
- How many are you starting with?
- How many do you need to take away?
- Do you have enough? If yes, then take away.
- If not, but you have some, add enough zero pairs, so you have enough to take away (some of them)
- If not, and you don’t have any, add enough zero pairs, so you have enough to take away (all of them)
6) Do LOTS of practice with these. There are practice questions in Math Makes Sense 7, or Math Focus 7, or Math Links 7 to support.
7) Follow up activity: Diamond sheet on subtracting integers (see below – imagine there is a box in the middle of the page where and integer subtraction sentence is written). The goal of this activity is to get students communicate their understanding in various ways, using the curricular competencies.
| Represent Visually | Explain in Words: |
| Describe a Real-Life Scenario | A Question You Still Have |
Day Five - Multiplying Integers with Tiles
The Learning Events should always be prefaced by focusing on the essential questions:
- What is balance?
- How do you achieve balance?
- How does change affect balance?
- How does change affect quantity?
Multiplying Integers with Tiles (Day Five)
1) Show students a simple multiplication expression (i.e. 3 x 2). Ask them to model it with integer tiles. Pay attention to how students model it (the arrangements they use). They will likely have six yellow tiles out, in various organizations – perhaps one row of six tiles, perhaps in two groups of three, perhaps in three groups of two. Ask students what the expression actually means. Is it the same as 2 x 3? Students will likely say yes, however, what is the same is the answer, not what it actually represents. Remind students that 3 x 2 can be read as “three groups of two,” and 2 x 3 is read as “two groups of three.” Ask students to then revisit their models – what have they actually modelled? Is it three groups of two? Is it three groups of positive two?
2) Next, have students model (+3) x (-2). Remind them that this means “three groups of negative two.”
3) Next, ask students to model (-3) x (+2). Students will likely model this the same way they did for (+3) x (+2). Some students will notice that there is now a negative sign involved and will start to incorporate negative tiles, and you will need to guide them to remember how to count the tiles – that they may be making zero pairs and not actually making the correct product. Allow students to struggle with this for a bit.
4) After some struggle, ask students what 3 x 2 is. They will know that 6 needs to be involved in the answer to the (-3) x (+2) question. But what about the negative? Remind them about how to say it; that it is somehow referencing three groups of two, but again, what about the negative? Guide students to understand that the negative means you have to take away three groups of positive two. But where are you going to take these groups from? This is where the six comes from. We know that 3 x 2 is 6, so we need to start with 6 zero pairs. Then take away the three groups of positive two. This will leave you with six negatives, or -6.
5) Repeat this with (-3) x (-2). This means “take away three groups of negative two.” Again, start with 6 zero pairs, because 3 X 2 is 6 and then take away three groups of negative two. You will be left with six positives, or + 6.
6) Repeat this activity with many different multiplication sentences, to have students practice the process.
7) Note – at this point, some students may notice, or start to generate a ‘short cut’ or rule for multiplication. Allow this to happen, but don’t focus too much on it. It’s more important for students to know what is happening through the process, than memorizing a short cut or rule.
8) After spending time with the tiles, move to paper and pencil practice. There are resources for this in Math Makes Sense 8, Math Focus 8 and Math Links 8.
9) Follow up activity: Diamond sheet on multiplying integers (see below – imagine there is a box in the middle of the page where and integer multiplication sentence is written). The goal of this activity is to get students communicate their understanding in various ways, using the curricular competencies.
| Represent Visually | Explain in Words: |
| Describe a Real-Life Scenario | A Question You Still Have |
Day Six - Dividing Integers - Connecting to Fact Families
The Learning Events should always be prefaced by focusing on the essential questions:
- What is balance?
- How do you achieve balance?
- How does change affect balance?
- How does change affect quantity?
Dividing Integers – Connecting to Fact Families (Day Six)
1) Once students are feeling confident with multiplication, move on to division. Remind students that division is the inverse of multiplication and review what a fact family is. Have students generate the fact family that goes with 3 + 2. Ask students what they notice about the numbers in the fact family (they are the same three numbers, just rearranged in different orders with different operations). Review a multiplication and division fact family as well (i.e. 2 x 5).
2) Next, have students look at fact families involving integers. Guide students to notice that a ‘regular’ fact family only involves three numbers, while an integer fact family will have more, since you can alternate the positive and negative sign in front of the numbers. Work with students to generate the fact family for 2 x 5, involving all the integers.
(+ 2) x (+5) = (+10) (-2) x (+5) = (-10) (-10) ¸ (+5) = (-2) (+10) ¸ (+5) = (+2)
(+2) x (-5) = (-10) (-2) x (-5) = (+10) (-10) ¸ (-5) = (+2) (+10) ¸ (-5) = (-2)
(+5) x (+2) = (+10) (-5) x (+2) = (-10) (-10) ¸ (+2) = (-5) (+10) ¸ (+2) = (+5)
(+5) x (-2) = (-10) (-5) x (-2) = (+10) (-10) ¸ (-2) = (+5) (+10) ¸ (-2) = (-5)
3) Once the fact family is made, ask students what they notice about it. Guide students to notice that they are more facts involved and have them speculate as to why. Also have them look at the division facts. Guide students to notice what is happening with the integer signs. Have students generate the ‘rule’ or short-cuts for multiplication and division of integers at this point.
- A negative times/divided by a negative gives you a positive.
- A negative times/divided by a positive gives you a negative.
- A positive times/divided by a negative gives you a negative.
- A positive times/divided by a positive gives you a positive.
4) Have students now create their own integer fact families, showing the relationship between multiplication and division. As an extension, have students create fact families using decimals, or larger numbers. Reinforce that the process is the same, no matter what kinds of numbers you use.
Day Seven - Order of Operations with Integers
The Learning Events should always be prefaced by focusing on the essential questions:
- What is balance?
- How do you achieve balance?
- How does change affect balance?
- How does change affect quantity?
Order of Operations with Integers (Day Seven)
1) Review what the order of operations actually is. Guide students to understand that it is much more than BEDMAS or PEMDAS; that the order of operations is a universal system used in mathematics. Talk about why this might be – why do we need a universal system?
2) Do some sample questions with students, demonstrating how to use the order of operations. Start by doing this without integers. Next, introduce the integers and remind them that it doesn’t matter what kinds of numbers are involved, you will always follow the same order of operations. Start with simple questions and move to more complex ones.
3) For student practice, give students a ‘target number’ and ask them to make as many order of operations equations as they can that will get to that answer. Give them some parameters, such as:
- Your equation must include at least one (or two, or three…) negative number(s)
- Your equation must include at least two (or three, or four…) different operations
- Your equation must include one (or more) set of brackets

The following resources are made available through the British Columbia Ministry of Education. For more information, please visit BC’s New Curriculum.
Big Ideas
The Big Ideas consist of generalizations and principles and the key concepts important in an area of learning. The Big Ideas represent what students will understand at the completion of the curriculum for their grade. They are intended to endure beyond a single grade and contribute to future understanding.
Core Competencies
 Communications Competency
Communications Competency
The set of abilities that students use to impart and exchange information, experiences and ideas, to explore the world around them, and to understand and effectively engage in the use of digital media
 Thinking Competency
Thinking Competency
The knowledge, skills and processes we associate with intellectual development
 Social Competency
Social Competency
The set of abilities that relate to students’ identity in the world, both as individuals and as members of their community and society
Curricular Competencies & Content
Curricular Competencies are the skills, strategies, and processes that students develop over time. They reflect the “Do” in the Know-Do-Understand model of curriculum. The Curricular Competencies are built on the thinking, communicating, and personal and social competencies relevant to disciplines that make up an area of learning.
Additional Resources
First People's Principles of Learning
To read more about First People’s Principles of Learning, please click here.
For classroom resources, please visit the First Nations Education Steering Committee.
